Positional Encodings I. Main Approaches

Large language models’ capabilities keep being pushed, and currently one of the areas of interest and active research is querying LLMs on progressively longer input sequences, up to hundreds of thousand and even a million tokens. In practice, that often means tweaking a model’s architecture to pre-train models with a modest context window and extending it as necessary at inference, optionally through some more additional fine-tuning. The main mechanism through which that is achieved is the Positional Embeddings* (PEs), or numeric representations that encode some notion of word order. We will be taking a closer look at them over this blog series, where in the first part we will characterize some common methods used to incorporate positional information into transformer models, and in the second part we will go over how these methods are used to extend context windows.

Solving word order insensitivity in the Transformer

Getting rid of recurrence was something that allowed to parallelize and scale attention-based models, letting the Transformer become the state-of-the-art architecture in NLP. On the flip side, that introduced the problem of having to endow these models with positional information, because they are inherently position-insensitive. The original Transformer architecture introduced the sinusoidal positional embeddings, visualized below, that are simply added to token embeddings before self-attention in each of the blocks.

The 128-dimensional PE for a sentence with the max length of 50. Each row represents a single PE. | Source

The intuition behind using the sine wave as a function of the embedding dimension and word position is that for word positions that are close by, their respective values at dimension i would be quite similar — imagine two dots near each other on the wave. Dots further apart would have different values, and that difference would be more pronounced in earlier _i’_s, that represent waves of higher frequencies; notice how most of the difference between positional embeddings (rows) is visible in the beginning, with the rest of them being pretty similar in the picture above. We refer interested readers to this blog that goes into more depth about sinusoidal PEs.

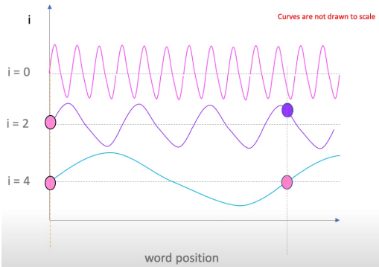
Intuition behind sinusoidal embeddings, i is, roughly, the embedding dimension | Source

There are at least two reasons behind this choice mentioned in the paper. One is that sinusoidal embeddings would make it easy for the model to understand relative positions, because the sine function has a nice property that for any k, sin(pos + k) could be represented as a linear function** of sin(pos). Another is that because whatever the position is, its sine and cosine values are going to be in the range [-1, 1], such positional encodings could extrapolate beyond the context length the model is trained with.

Sinusoidal PEs are fixed, which saves on computation, they have some useful properties, and they were adopted in many models later. However, this solution to the word order issue in transformers was not the only one, and further research aimed to analyze it and improve upon it.

Fully learned absolute PEs

It is mentioned in the Transformer paper that in experiments, fully learned embeddings performed similarly to the fixed sinusoidal ones. Fully learned absolute positional embeddings that are also added to token embeddings were not a novel idea, and the later transformer models like GPT***, BERT and RoBERTa go back to that practice. Reasons for opting for this conceptually simpler version could be, for example, that when training a model on vastly more data, it would allow such embeddings to learn richer representations than the fixed sine pattern; this blog discusses some more hypotheses.

While fully learned absolute PEs are easy to implement and can be quite expressive, they might fail to generalize, and in terms of being extendable, no methods have been proposed to utilize them to extend the context window.

Fully learned relative PEs

It is interesting to note that the authors of the original Transformer paper cite the ability to capture relative position information as one of the reasons for choosing the sinusoidal position embeddings, although they are, strictly, absolute embeddings. Intuitively, most of the time what we really care about is indeed the relative position of two words in a sentence, whether they both occur at positions 2 and 5, or 6 and 9, or 102 and 105. Practically, too, assigning fixed or learned representations to absolute positions is just not meaningful in some cases, such as packingmultiple sequences into a single input, or combining multiple inputs to achieve a longer context window.

The team behind the Transformer paper quickly introduced their version of relative position embeddings, which are learned, and since the focus is on the pairwise word relationships rather than individual words, their computation is moved into the self-attention mechanism, where pairwise scores between queries and keys are computed. Furthermore, because dependency between tokens is likely to fade with distance, they clip the maximum distance between two positions to k, which potentially allows the model to generalize to longer context lengths than seen during training, as any token beyond k each way would have the PE of k. This approach was shown to improve BLEU scores for machine translation tasks and inspired further research into relative PE methods.

Absolute vs Relative PEs | Source (modified)

A notable variation of relative PEs, that we will come back to later, is the T5 bias, where relative position embeddings are simplified to single scalars that are learned and added to the corresponding query-key dot product used to compute attention weights.

Sinusoidal Relative PEs

The idea to keep some nice properties of sinusoidal embeddings, but use them in a relative fashion was adopted by multiple models as well. Transformer-XL was one of early works explicitly concerned with extending the effective context window to model longer texts. While the authors achieve that by combining multiple inputs with recurrence, they also propose a novel relative position embedding scheme to accommodate that. In the computation of self-attention, they use trainable parameters to represent positional information of the queries as well as relative sinusoidal encodings to represent positional information of the keys.

In NEZHA, a BERT-based model for Chinese language, authors utilize a similar self-attention computation scheme with relative PEs as in Shaw et al., but derive the positional encodings from the sine and cosine functions similarly to the original Transformer model. Authors report moderate, but stable performance gains of using their version of sinusoidal relative PEs over learned relative PEs across several NLU tasks.

Which PE is best?

The PE methods we mentioned so far vary along the ‘absolute vs. relative’ and ‘learned vs. fixed’ axes, and it would be helpful to get an idea of their relative performance. These methods were implemented in different models and/or different languages and often along with other adjustments, which makes it hard to do so. This problem is tackled in Wang et al., where variants of BERT are trained with PE methods we have mentioned so far and evaluated on multiple tasks.

Sinusoidal vs. Learned

BERT with its original fully learned absolute PEs outperforms Transformer-style sinusoidal absolute PEs in classification tasks (as measured on GLUE), which could be evidence that the PE at the first position, corresponding to the special [CLS] token used for downstream classification, learns richer information than strictly position. Absolute sinusoidal PEs, however, outperform the fully-learned counterparts in span prediction (SQuAD 1.0 and 2.0), where all tokens are taken into account.

Absolute vs. Relative

Absolute PEs were found to perform better on classification, while relative PEs performed better on span prediction tasks. The authors see the reason for that in such tasks requiring understanding of local context, while classification tasks require the ‘gist’ of a whole sequence and rely on the [CLS] token for that, which is always at a fixed position. Another hint that for classification tasks position information is not as crucial is that removing PEs was demonstrated to hurt performance in GLUE tasks only slightly, while significantly decreasing scores in SQuAD.

RoPE: modern fixed PEs

Rotary position embeddings were the innovation that combined in it many of the desirable properties that we have discovered so far: including absolute and relative positional information, the use of trigonometric functions, continuity, fusing positional information into the self-attention mechanism, and importantly, extendability.

The idea behind RoPE is to express the inner product between a query at position m and a key at position n through a function that would only take their respective embeddings and the relative position m-n. Specifically, queries and keys vectors are rotated (technically, multiplied with rotation matrices) according to their absolute positions in a sequence. However, because of the predictable step-wise rotation, the angle between two vectors at positions 1 and 3 or 101 and 103 would remain the same, i.e. their relative position information would be naturally encoded. The fact that rotation matrix is multiplied with vectors, such that it does not change the vector norms, makes it easier for a model to learn, compared to when position vectors are added directly to token embeddings.

Embeddings with positional information encoded with sinusoidal (left) and rotary (right) PEs | Source

In practice, for vectors with much higher dimensionality, RoPE implements the following trick, illustrated below. Query and key vectors get split into chunks of size 2, and each chunk multiplied with the 2x2 rotation matrix, with decreasing speed of rotation. The rotated chunks get concatenated to get the resulting vector, notice how they get tinted with their respective position’s color in the bottom right in the picture below.

Implementation of RoPE | Source

The main benefits of this method are as follows. Firstly, it allows for extending context length to an arbitrary number of tokens theoretically (and as we will see later, to an impressive number practically), because the attention score depends only on relative distance between tokens. Secondly, unlike relative PEs we saw before, RoPE allows for graceful decrease of inter-token dependency without cut-offs. Thirdly, due to how PEs are incorporated into the attention mechanism, they can work both with regular softmax attention and linear attention — and that is, reportedly, the only existing method to enable that.

In practice, RoPE allowed for fast convergence and significant performance gains, especially on tasks with longer contexts, and was adopted in models like LLaMA, GPT-NeoX, PaLM, Orca and Dolly.

ALiBi: the efficient T5 bias

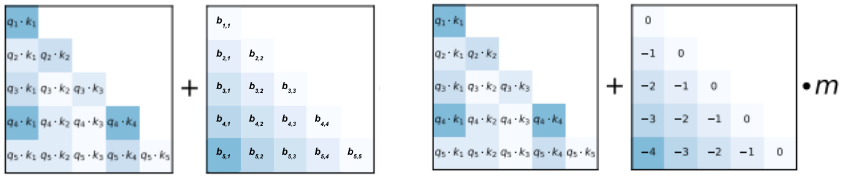
It was discovered that in experiments, the T5 bias actually was the most effective method of extending the context window at inference, and it was further developed into ALiBi, or Attention with Linear Biases. Noticing that T5 bias is slow to train, they instead fix all relative bias parameters and add a per-head slope m, that is also fixed.

T5 bias (left 2) and ALiBi (right 2) | Source (T5 bias drawn off of description)

ALiBi showed remarkable extrapolation ability, keeping the inference perplexity stably low for context sizes up to 16k tokens, with a model only trained on the context window of 512 tokens, as seen in the graph below. Note how the sinusoidal embeddings did not live up to original authors’ expectations — they were reported to only be able to extend to a few dozen tokens beyond the initial context window.

Extrapolation for models trained on 512 tokens | Source

Ease of implementation, computational efficiency and the extrapolation performance made it the PE of choice in models like MPT and BLOOM.

In conclusion

This is by no means a full account of methods of injecting positional information in transformer models, with some other methods including using graph or tree structures, kernels, randomness, complex representations of word embeddings, etc. We hope that the methods described should equip the reader with a rough understanding of the main concepts necessary to talk about extending context windows through PEs. So far, we have only seen experiments extending the context window at inference quite moderately, and in the second part of this series, we will see how these concepts are leveraged to allow extensions to tens and hundreds of thousands of tokens in modern LLMs.

Footnotes

*Some texts reserve the term positional encodings for fixed representations and call learned ones positional embeddings. We will adopt that distinction where necessary and we will use the contraction PE as an umbrella term to refer to both.

**sin(pos + k) = sin(pos)cos(k) + cos(pos)cos(k)

***The modern GPT models, at least up to GPT-3, are reported to use that exact method.

Positional Encodings I. Main Approaches was originally published in MantisNLP on Medium, where people are continuing the conversation by highlighting and responding to this story.